Théorème de Norton

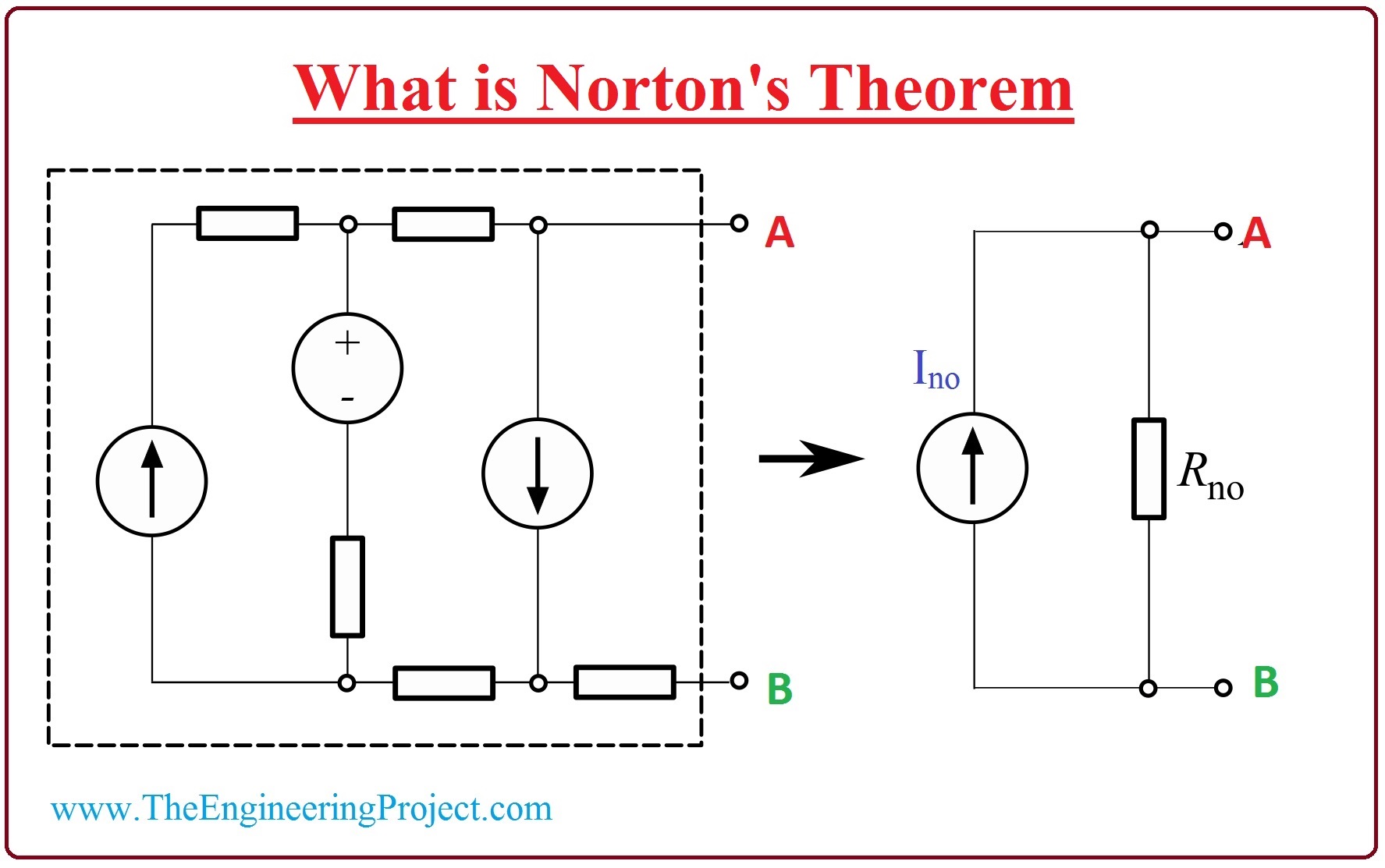
Le théorème de Norton pour les réseaux électriques établit que tout circuit linéaire est équivalent à une source de courant idéale $I_{\mathrm {N} }$ , en parallèle avec une simple résistance $R_{\mathrm {N} }$ .

Le théorème s'applique à toutes les impédances, pas uniquement aux résistances. L'énoncé de ce théorème a été publié en 1926 par l'ingénieur Edward Lawry Norton (1898-1983).

Communément :

le courant de Norton est le courant entre les bornes de la charge lorsque celle-ci est court-circuitée, d'où I_cc = I (court-circuit) ;
la résistance de Norton est celle mesurée entre les bornes de la charge lorsque toutes les sources sont rendues inactives, en court-circuitant les sources de tension et en débranchant les sources de courant. En d'autres termes on le remplace par un interrupteur fermé les générateurs de tension et par un interrupteur ouvert les générateurs de courant.

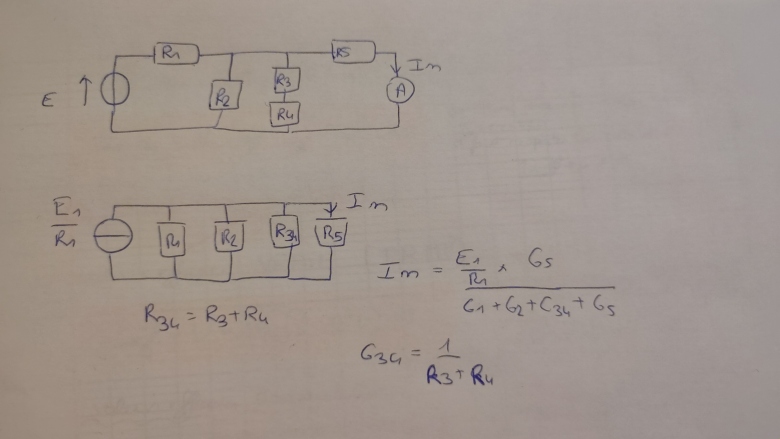
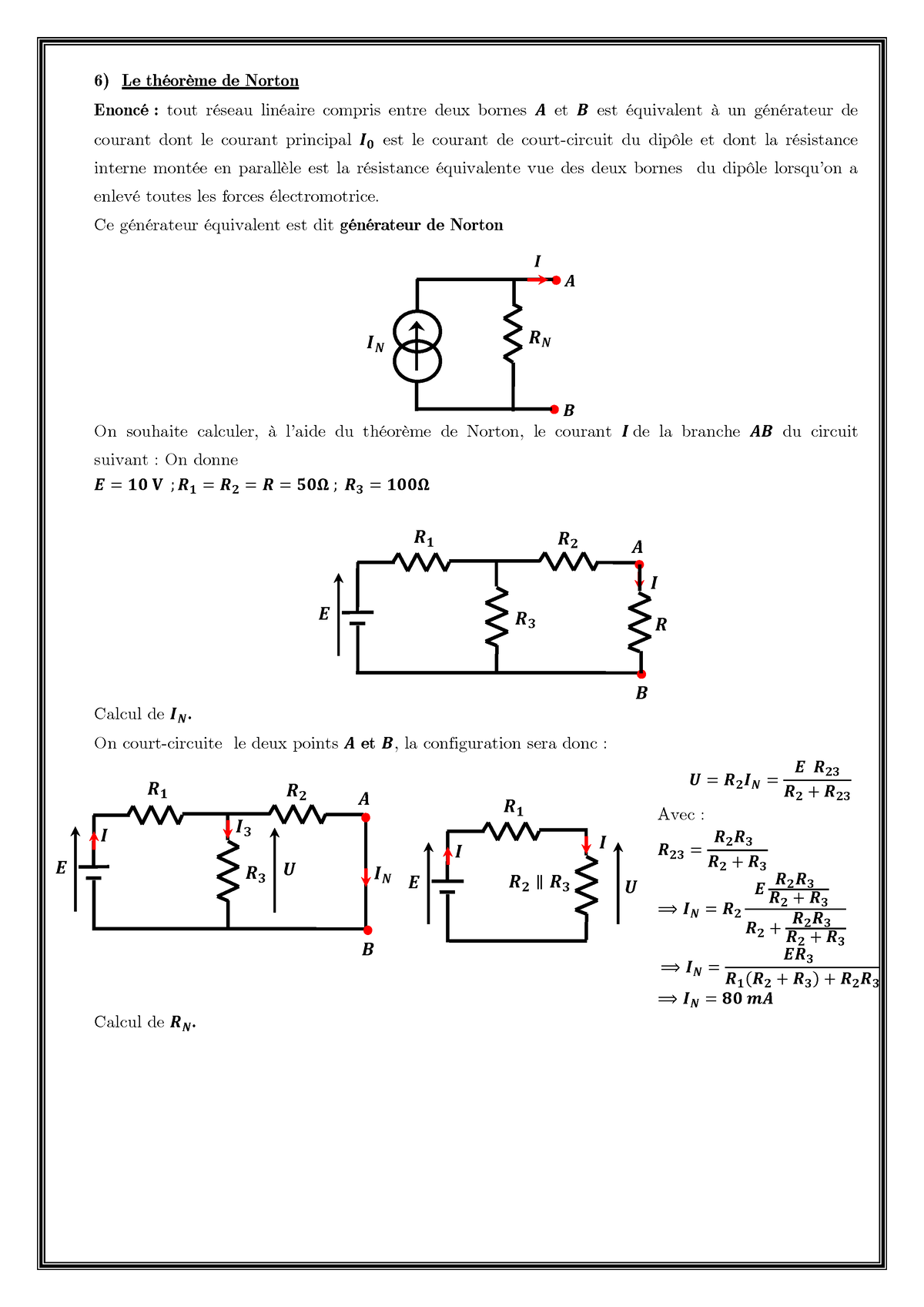
Exemple

En (a) : circuit original

En (b) : court-circuit entre les bornes a et b pour trouver le courant Norton $I_{\mathrm {N} }$

On calcule d'abord le courant total délivré par la source de tension

I_{\mathrm {total} }={\cfrac {V_{1}}{R_{1} \left({\cfrac {R_{2}\cdot R_{3}}{R_{2} R_{3}}}\right)}}=4{,}54\ \mathrm {A}

On trouve ensuite le Courant de Norton par la formule du diviseur de courant.

En (c) : On neutralise le générateur. Ici on le remplace par un interrupteur fermé. On ouvre le circuit entre les bornes (a et b), le courant passant par $R_{\mathrm {3} }$ est donc nul. On cherche alors la résistance équivalente du circuit $R_{\mathrm {N} }$ .

R_{\mathrm {N} }=R_{3} \left({\cfrac {R_{2}\cdot R_{1}}{R_{2} R_{1}}}\right)=3{,}67\ \Omega

En (d) : circuit équivalent de Norton

Conversion entre un circuit de Norton et de Thévenin

On passe directement d'un circuit de Norton à un circuit de Thévenin et inversement, en appliquant la loi d'Ohm et en changeant la place de la résistance. On a :

de Norton à Thévenin:

V_{Th}=I_{N}\times R_{N}

R_{Th}=R_{N}

de Thévenin à Norton:

I_{N}=V_{Th}\div R_{Th}

R_{N}=R_{Th}

Applications

Le théorème de Norton permet de remplacer un dipôle par un modèle équivalent ne comportant que deux dipôles en parallèle. Il est donc particulièrement bien adapté pour déterminer le modèle équivalent d'un ensemble de branches en parallèle. Le théorème de Millman peut donc s'en déduire rapidement, de même que l’intensité du courant dans le neutre pour une installation triphasée.